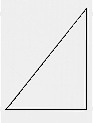
Next, the theorem of Pythagoras.
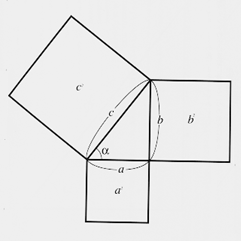
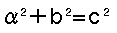
And
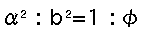
I thought "Oh, this is the golden section," then, I woke up.
This means
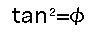
It's beautiful, but is this true?This must be a dream of the Great Pyramid's angle of inclination which I've been thinking of since I was twenty.
So I checked out if my dream was true. I found in a book, Herodotus heard from an Egyptian priest that "Each area of the Great Pyramid's side equals a quadrilateral which has a side of the Pyramid's height.' I can figure out the golden triangle from this story.
an area of the Pyramid's sideione of the four sidesjis

which means
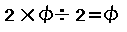
On the other hand, the area of a quadrilateral which has a side of the Pyramid's height is
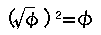
This golden triangle is the same as the one I dreamed of.
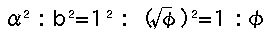
But could this be a real golden triangle? Actually, I found a Finabotch progression which I asked my friend to calculate in the computer center of my university. It's no trouble for me to calculate the golden section.
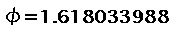
If this is correct,
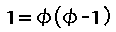
In this case, 1=0.99999998.
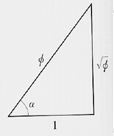
If the angle of this golden triangle is ¿, I can think of the next expression.
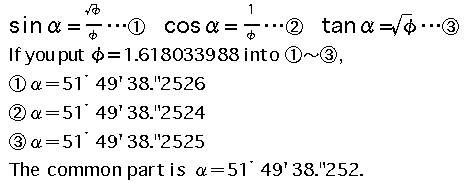
The periphery of this golden triangle Pyramid is the same as the circumference whose radius is the Pyramid's height?
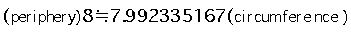
The Great Pyramid's angle of inclination is
 <BR>
<P>
jIf the translation is not enough or incorrect, please e-mail
<A HREF=) CYCLE.
CYCLE.